El Teorema de Pitágoras:
El Teorema de Pitágoras nos dice que en los Triángulos Rectángulos, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos. Esto es:
donde a y b son las logitudes de los catetos y c la longitud de la hipotenusa.
Esta fórmula es muy útil para calcular la longitud de uno de los lados de un triángulo rectángulo si se conocen los otros dos:
Esta fórmula es muy útil para calcular la longitud de uno de los lados de un triángulo rectángulo si se conocen los otros dos:
- a = √(c2 - b2)
- b = √(c2 - a2)
- c = √(a2 + b2)
- c = √(a2 + b2) = √(42 + 32) = √(16 + 9) = √25 = 5
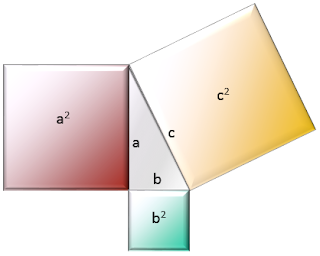
ElTeorema de Pitágoras se puede representar con superficies cuadradas correspondientes a cada uno de los lados de manera que la suma de los que tienen la longitud de los catetos es igual al de la superficie del que tiene el lado de la hipotenusa.
En el ejemplo de la izquierda, si sumamos la superficie que ocupa a2 y b2 comprobaremos que es la misma superficie que c2.
Las Bisectrices de un Triángulo son las rectas que partiendo de cada uno de los vértices dividen sus correspondientes ángulos internos en dos partes iguales .
El Teorema de Pitágoras toma el nombre del matemático que vivió en la antigua grecia en el siglo VI antes de Cristo pues por tradición se supone que fue el primero en demostrarlo. Ahora bien, existen indicios de su conocimiento en épocas anteriores.
Este teorema es quizás sobre el que más demostraciones diferentes ha tenido, incluida una demostración hecha por el presidente de los Estados Unidos James Abram Garfield (1831-1881).
Ejercicios:
- Calcular la longitud de la hipotenusa de un triángulo rectángulo cuyos catetos miden 3 y 2.
- Calcular la longitud de un cateto si la hipotenusa mide 5 y el otro cateto mide 4
versión 1 (01/12/2015)

No hay comentarios :
Publicar un comentario